どうも、カタミチです。
さて、今日も「最短コースでわかる ディープラーニングの数学」のひとり読書会、やっていきたいと思います。
10-8. プログラム実装(その2)

なぜだ…なぜ損失関数が収束しない…!?
ヒントは重み行列の初期値にありました。これまでずっと、重みの初期値は1で通してきましたが、やはり初期値をより適切に与えることはできるようですね!
用いるのは、「He normal」と呼ばれる方法のようです。どんなものかと言うと…
平均0、分散1の正規分布乱数(値の発生確率が正規分布に従うような乱数)を一定値(\( \sqrt{\frac{N}{2}} \):Nは入力データの次元数)で割った値を重み行列の初期値とする。
というものです。
正規分布乱数か…。さぞや生成がめんどくさいと思いきや、NumPyの関数で用意されているようですね。一行で導出できました。これによって、ひとつひとつの要素の初期値が違う、雑然とした重み行列(\(\boldsymbol{V},\boldsymbol{W}\))ができました。
これまでの整然と1が並んだ重み行列の初期値から、一見するとゴチャっとした初期値に変えたことで何が起こるのか…?さぁ、学習処理を実行してみましょう…
どん!
はい、今回も3分くらい掛かりました。
損失関数のグラフを見てみましょう…
どどん!
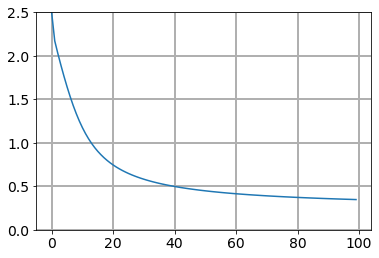
おー、下がってる!
初期値パワー恐るべし。
しかし、なんでこの初期値の方が損失関数が下がりやすいのか?についてはよく分かっていません。後の章にも出てくるらしいとあったので、そこでもう少し見てみますかね〜。
これでついに、ラスボスも完全攻略ですかねー。
精度のグラフを見てみましょう。
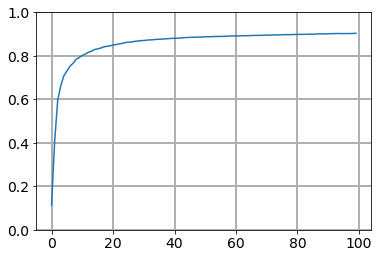
む…?
精度0.9付近。つまり90%程度ってことになります。まぁ、10回に9回は当たるってことなので、ここで妥協しても良い気もするんですが、実用面を考えると少しもの足りない結果…ってことになりますかね。
ということで、さらに精度を上げるべく、最後のひと押しだ!(つづく)
ということで
やはり、重みの初期値にも工夫があったんですねー。第7章で出てきた時の疑問は、これで解消されました。と、同時に、初期値にも奥深さがあることを知って、勉強の裾野の広さを改めて感じさせられました。
さて、チューニングもあとひと息ですね。頑張っていきたいと思います!
ではまた。