どうも、カタミチです。
さて、今日も「最短コースでわかる ディープラーニングの数学」のひとり読書会、やっていきたいと思います。
今日は9章「ロジスティック回帰モデル(多値分類)」の続きからですね。さて、理解を進めていきましょう…!
9-3. 重み行列

さて、今回のキモが「分類器が複数になった」というところなんですが、これはつまり「N個のモデルが並列に稼働している」と捉えるようですね。それに伴って、重みベクトルもNセット分必要になります。それを表現するために出てくるのが…行列の考え方ですね。今回は、アヤメを3品種に分類したいということなので、Nセット=3セットということになります。この時の出力データを\(u_0,u_1,u_2\)とすると、それぞれに対して式ができますね。
こんな感じです…どん!
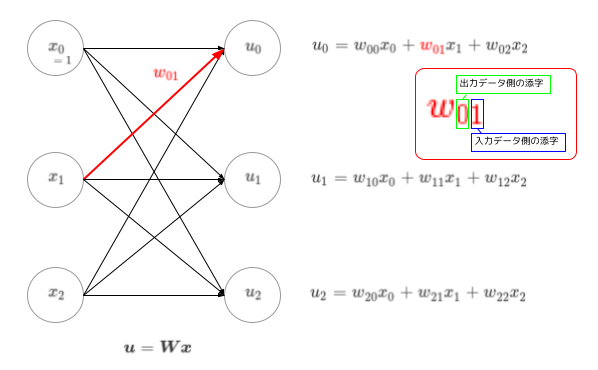
混乱しないように気をつけたいのは、重み\(w\)の添字です。例えば\(x_1\)から\(u_0\)に向かう時にかかる重みは\(w_{01}\)と表現されています。矢印の向きだけ見ると添字の順番が逆のほうが分かりやすいんじゃね?と言う意見もあるようですが、この順番の方が、\(w\)たちをまとめて一つの行列\(\boldsymbol{W}\)で表した時に、1つ目の添字が行を、2つ目の添字が列を表すこととなるので直感的に分かりやすいです。…まぁ、実際のところ色んな書き方があって統一されていないらしいですが(求ム規格化)。
さて、式は3つできるんですが、行列表現を使うとこれらを1つにまとめることができます。上の図にも書いていますが、コレですね。
$$ \boldsymbol{u} = \boldsymbol{Wx} $$
要素で表現すると…
\(\boldsymbol{u}=\left(\begin{array}{c}u_0\\ u_1 \\ u_2\end{array}\right)\)
\(\boldsymbol{W}=\left(\begin{array}{c}w_{00} & w_{01} & w_{02}\\ w_{10} & w_{11} & w_{12} \\ w_{20} & w_{21} & w_{22}\end{array}\right)\)
\(\boldsymbol{x}=\left(\begin{array}{c}x_0\\ x_1 \\ x_2\end{array}\right)\)
ですね。
9-4. softmax関数
さて、とりあえず入力値に重みが付いて予測モデルっぽいものができましたが、その値をそのまま\(yp\)とはせずに\(u\)にしているってことは…
はい、今回も活性化関数が間に挟まります。分類器が複数になったことによって複雑化したものの、それぞれの分類器は\(0\)or\(1\)を正解値として取るので、\(yp\)はやっぱり\(0\)〜\(1\)の確率表現にしたいところです。
いったい、どんな関数が間に挟まると言うんだ…!?(ざわ…ざわ…)
それが…
softmax関数だ!
…いや、見出しに書いてあるから最初からバレてるとか言わないで(涙)。
さて、そんなソフマップ…じゃなくてsoftmax関数の定義はこうでしたね。
$$ \left\{ \begin{array}{c} y_0=\frac{exp(u_0)}{g(u_0,u_1,u_2)} \\ y_1=\frac{exp(u_1)}{g(u_0,u_1,u_2)} \\ y_2=\frac{exp(u_2)}{g(u_0,u_1,u_2)} \end{array} \right. $$
$$ g(u_0,u_1,u_2)=exp(u_0)+exp(u_1)+exp(u_2) $$
ん?よく見るとこれ…
そのまま使えそうじゃん。
逆に言うと、多値分類問題を解くために編み出された関数…ってことなのかもしれませんね。あまりにも当てはまりが良すぎる。
ということでこれで、ロジスティック回帰の多値問題の予測モデルが完成です。
ちなみに、softmax関数の偏微分も既に導出済みなので一応載せておきますかね。
$$ \frac{\partial y_j}{\partial u_i}= \left\{ \begin{array}{c} y_i(1-y_i) & (i=j) \\ -y_iy_j & (i \neq j) \end{array} \right. $$
たぶん、後で使う…はず。
ということで
2値問題で苦労したおかげで、多値問題の予測モデルは比較的イメージをそのまま拡張するだけで理解できました。続いては損失関数ですね。また尤度関数が出てくると思いますが、詰まるポイントはあるかなー。楽しみです。
ではまた。