どうも、カタミチです。
さて、今日も「最短コースでわかる PyTorch&深層学習プログラミング」のひとり読書会、やっていきますかねー。
2章も後半戦に入ってきましたね。気合い入れていきましょう〜
2-4. 2次関数の勾配計算

さて、今回はコードいじっていきましょう。
最近、だんだんとコードいじるのが楽しくなってきました。私、社会人になって最初の職種がプログラマーだったので、根っこのところではやっぱりコード書くのが好きなのかもしれません。まぁ、15年くらいブランクがありますが(汗)。
今回も、\(y = 2x^2 + 2\)を例にやっていくみたいですね。せっかくなので別の関数でやろうとも思ったんですが、ひとまずこいつでやっていきますかねー。
前節によると、まずは勾配計算したい変数を定義するんでしたね。ここでは\(x\)とするようです。
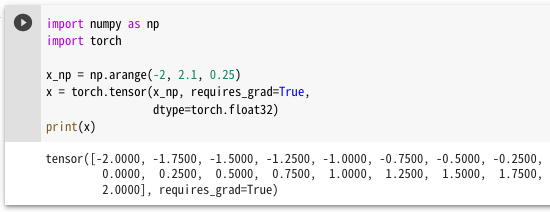
これも前回までに出てきたヤツですが、-2から2までの0.25刻みの数値として定義するようです。違うのは、Tensorに突っ込む時に、引数に「requires_grad」ってやつを「True」で指定しているところですかね。ひとまずはオマジナイってつもりで見ておきますかねー。あと、型変換する場合は「dtype」って引数を使うやり方もあるようですね、ふむふむ。
ともあれ、これで階数1のテンソルがひとつできました。
次に、テンソル変数間での計算をするんでしたね。式を見てみましょう。

…うむ、定義した\(x\)をそのまま式に突っ込んでますね。結果変数の\(y\)がどうなってるかをprintで見てみると、どうやらこちらもtensorになったようです。普通の数式を書いておいて変数をテンソルにしておけば計算結果もテンソルになる…と。なかなか便利ですね。なんか「grad_fn=<AddBackward0>」ってのがくっついてるのが気になりますが、おいおい分かる…かな?
あと、直後に\(z\)というのが定義されています。\(y\)の値をすべて足し上げたものらしいんですが…
なぜ足し上げるんじゃ〜
これはちと手強いです。説明上は「勾配計算のためには、最終値はスカラーの必要があるため、ダミーでsum関数をかける」とあります。とりあえず、最後をスカラーにするために帳尻合わせで足し上げた…っぽいですね。とりあえず慣れるしかないかなぁ。
ちなみに、ここにも「grad_fn」がくっついていますね。「=<SumBackward0>」ってことで、値が変化していますね(ふむ)。
さて、3つ目の手順は、計算グラフの可視化です。どうやら「torchviz」というライブラリを使うようなんですが、コードをそのまま実行してみたら、インストールできてなかったので一度エラーになってしまいました(汗)。
ということで、ピップエレキバンを貼って…

実行!(ピップエレキバンとは)
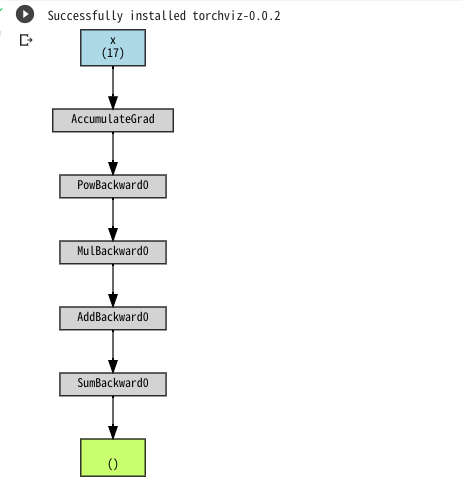
おお、なんか出た!
どうやら、出発点の\(x\)から計算結果の\(z\)に至るまでの過程が書かれている…らしいです。これにどんな意味があるのか、ちょっとまだ理解できないですねー。
…ん?よく見ると「AddBackward0」とか「SumBackward0」ってやつは、上のコードの実行結果の「grad_fn」ってやつで出てきましたね。「AddBackward0」より上のハコのやつはコードの実行結果には出てきていませんが、計算過程では出てきてる、ってことでしょうねー。
今のところ、このフロー図がどう役に立つのかは分かりませんが、ひとまずこんなやつが出力できるってことは覚えておきますかねー。
で、いよいよ勾配計算です。どんな複雑な関数が飛び出すのか…?
どん!
![]()
…はい、これだけです。結果変数\(z\)に対して「backward関数」を呼び出すだけで勾配計算ができるようですね!
ちなみに、勾配計算にはスカラーしか取れないということだったのですが、一応、お約束ってことで「y.backward()」も試してみました。
結果は…
どん!
![]()
訳:勾配はスカラーの結果に対してしか生成できへん言うのが暗黙のルールやって言うたやろ!
…怒られました。すみません(素直)。
勾配計算が終わったので勾配値を取得してみます。どうやら「x.grad」って書けば勾配値になるらしいです。やってみましょう。
どん!

おー、微分されてますね、これは。前にも同じ結果を見た記憶があります。
グラフ書いてみると…
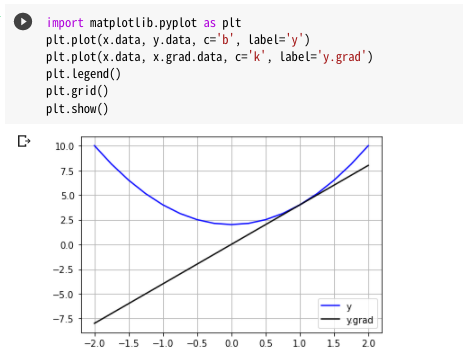
うん、こっちも前に見たグラフですね。バッチリです。
で、最後に勾配値の初期化が必要ってことで…

これで締めるのがお作法のようです。鍋の最後をラーメンで締めるようなもんですかね(誤解を招く例え)。
ちなみに、初期化しないと前の値が残ってしまって、2度目の勾配計算の時に1度目の値が足されてしまってワケ分からんことになるみたいです。
追記:
本節について、どうやら補足記事が書かれているようなので、合わせて紹介しておきます。
・書籍「Pytorch&深層学習プログラミング」2章補足 sum関数で微分計算ができる理由 - Qiita
・書籍「Pytorch&深層学習プログラミング」2章補足PART2 sum関数をmax関数に置き換えると何がおきるか? - Qiita
\(z\)を\(x_k\)で偏微分した結果が…
\( \frac{\partial z}{\partial x_k} = f'(x_k) \)
となり、\(y_k\)を\(x_k\)で微分したものである\(f'(x_k)\)と一致するってことが、sum関数が使われている理由ってことのようです。少しだけ理解に近づいた…かな。
ということで
流れは分かりましたが、ひとつひとつの意味をしっかり理解できたかと言うと…怪しいです。まぁ、この先繰り返し出てくるロジックだと思うので、徐々に慣れていきますかねー。
とりあえず、次の節でも勾配計算をやるようなので、もう少し慣れる…かな?
ではまた。