どうも、カタミチです。
さて、今日も「最短コースでわかる PyTorch&深層学習プログラミング」のひとり読書会、やっていきますかねー。
今日もPythonのツボの章の続きですね。
行ってみよ〜
1-4. 「微分」とPythonでの「数値微分」の実装
今日は微分の話ですね。微分は「ディープラーニングの数学」の中でも最もページ数が割かれていた数学的要素です。PyTorchでは、微分計算は内蔵されてるみたいなので、この節で出てくる内容は、実際をコードで書く感じではないみたいですね。とはいえ重要なのでちゃんと理解しておこう!ということのようです。
微分と言えば\( \lim\)の式ですが、PyTorchでは「数値微分」を使うようです。比較的最近やったやつですね。
【ひとり読書会】ディープラーニングの数学(第38回) - まったりAI勉強記
「数値微分」とは、数式の微分結果を数式で表すのではなく、実際に\(h\)に微小な数値を代入して、近似値を求めるやり方ですね。
使う式は、本来の微分の式と違い、こんな感じ。
\( f'(x) \simeq \lim_{h \to 0} \frac{f(x+h)-f(x-h)} {2h} \)
「数値微分」の場合、本来の微分の式よりこっちの式の方が精度が良さそう…って点は、前回勉強した上の記事の時に考察&実験しましたが、本章の章末にあるコラムでもしっかり説明されていたので理解がより深まりました。
ちなみに「数値微分」に対して数式レベルで行う微分は「解析的な微分計算」と言うようです。
さて、Pythonでの実装を見てみますかねー。

…む、初めて見る書き方。
微分の公式は4行目に書かれてますね。で、微小な\(h\)ってのが3行目。\(1e-6\)ってのは、\(1 \times 10^{-6}\)ってことみたいです。\(0.000001\)って書くよりスマートですね。覚えとこ。
で、その微分の式を返り値とする関数(diff)を取り囲むように、外側に関数(fdiff)が定義されています。ちなみにこの関数名は恐らく、「微分」を表す英語である「differential」から取ってるんでしょうね。「differential」って、「差、差分」みたいな意味だと思ってたんですが「微分」って意味もあるんですね。なかなか興味深い(ふむ)。
どうやら、この「fdiff」の引数に微分したい関数を放り込むと、微分された式「diff」が得られるって寸法のようですね。この書き方さえ知っていれば、各種微分の公式を苦労して導く必要はない…というわけですね。…ちょっと寂しい(数学脳)。
さて、前節で使った関数を今回も使いましょう。

\(f(x)=2x^2+2\)ですね。「解析的な微分計算」によると、\(f'(x)=4x\)って事になりますね。
ということで、この関数をfdiffに突っ込んでみましょう。

2行目の式がまさに微分の式って事になりますね。あらかじめ与えた\(x\)に対するy'の数値は…
![]()
はい、こうなりました。解析的な微分計算に\(x\)を代入した結果と一致しますねー。
ということで、基本的にはここで終わりなんですが、数値微分の結果を元の式とともにグラフで書いてみると…
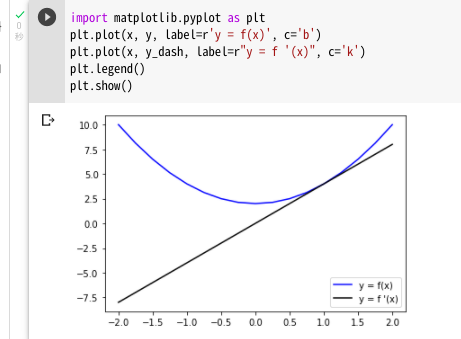
はい、やっぱり解析的な微分計算と同じ風味の結果が得られていますね。
ついでに、同じ要領で例題2。

どんな実数を入れても0から1の値を返す…でお馴染みの「シグモイド関数」ですね。
同じように数値微分に放り込んでみましょう。
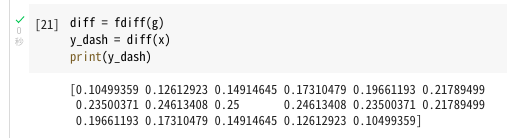
できましたね。ちなみに\(x\)の値はそのまま流用してます。グラフ書いてみましょう。
えい!
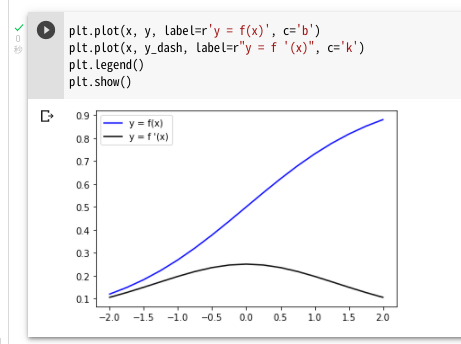
解析的な微分計算との対比の詳細を書くのはやめときますが、一致しますね、はい。
シグモイド関数は、微分すると最大値が落ち込んで「勾配消失」が起こる…ってのはこれを見るとよく分かりますね。
ということで
1つ1つの節が割と重いので、なかなか進みませんね(汗)。まぁ、毎回何かしら得られるものがあるのでよしとしますかねー。今回は、引数として関数を与えることができることを利用して関数の関数が表現できるってのが得られた知識です。
さて、1章もあと2節。頑張っていきますかねー。
ではまた。