どうも、カタミチです。
さて、今日も「最短コースでわかる ディープラーニングの数学」のひとり読書会、やっていきたいと思います。
今日は、9章「ロジスティック回帰モデル(多値分類)」の最後の節、プログラミングのところですね。張り切って行ってみよう〜
9-8. プログラム実装

今回も、サンプルコードを1行1行読んで理解するということをやってみました。
NumPy関連では、飛び飛びの列を指定するやり方が使われていたり、「c_[ ]」ってのを使って配列を作っていたりと、いくつかのワザが使われていました。
あと、正解値が0に該当するデータ系列番号の入力データだけを抜粋する書き方として、「(抜粋後入力データ行列) = (入力データ行列)[正解データベクトル == 0]」みたいな書き方がされていて、こんな書き方もできるんだなー、と驚きました。
また、今回の多値分類で初登場の「OneHotベクトル」を作る作業は、scikit-learnの関数でカンタンにできるようですね(メモメモ)。
ちなみに今回は、訓練データとテストデータを半分ずつに分けるみたいですね。前章で、だいたい7:3か8:2が一般的…とあったので、今回は例外的な感じですかね。
コードを読み進めていくと、softmax関数の定義の部分で入力値をそれぞれ入力値の最大値から引き算した値を使っているところがありました。小一時間、意味がわからず悩んでいたんですが、本書に戻って見たら答えが書いてありました。値が大きくなりすぎるとオーバーフローが起きて処理ができなくなる可能性を避けるために、値を小さくしてるらしいです。ちょっとした加工処理ですね。
しかし、勝手に引き算したら結果が変わってしまうのでは…?と思うんですが、本書によると、入力値をそのまま使うのも引き算後の値を使うのもsoftmax関数の値は変わらないらしいんです。…ほんとかいな。
ちょっとやってみましょう。
今回の例題に合わせると、入力データは3つ\( (x_0,x_1,x_2) \)。出力データも3つ\( (y_0,y_1,y_2) \)。softmax関数は…
\( y_0= \frac{exp(x_0)}{exp(x_0)+exp(x_1)+exp(x_2)} \)
ですね。(\(y_1,y_2\)も同じ感じ)
ここで、\(x_0,x_1,x_2\)の中で\(x_2\)が一番大きい値だとすると、最大値で引き算した司式は…
\( y_0= \frac{exp(x_0-x_2)}{exp(x_0-x_2)+exp(x_1-x_2)+exp(x_2-x_2)} \)
ですね。変形してみましょう。累乗の引き算は底の割り算で表現できるので…
\( y_0 = \frac {\frac{exp(x_0)}{exp(x_2)}} {\frac{exp(x_0)}{exp(x_2)}+ \frac{exp(x_1)}{exp(x_2)}+ \frac{exp(x_2)}{exp(x_2)}} \)
あっ…
分子と分母から\(\frac{1}{exp(x_2)}\)を括りだすことができるので、括りだしてから約分すると…
\( y_0= \frac{exp(x_0)}{exp(x_0)+exp(x_1)+exp(x_2)} \)
確かに、元の式に戻りましたね!
その後の式は、ベクトルが行列になったりはしているものの理解できない部分はなく…無事に学習をパートを完了。
で、今回も損失関数の減衰具合と正解率(accuracy)の上がり具合をグラフ化するソースコードが組み込みれていたのですが、コードをよくよく見てみると…
どうも、テストデータに割り振ったデータを損失関数と正解率のグラフとして書いてみるようです(コードを読み違えていたらすみません)。確かにコレだと、グラフ見てそのまま評価できそうですね。イテレーションを回すついでにデータを貯めるのに都合がいいように、訓練データとテストデータを同数に割った…という感じですかねー。こういうやり方もあるのか(ふむふむ)。
で、そんな感じで出たきた損失関数と繰り返し回数のグラフがこちら。
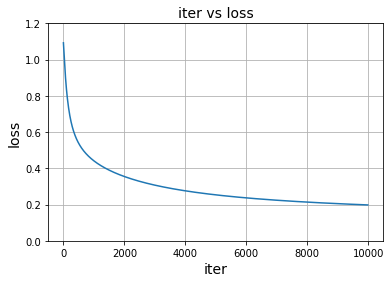
うん、順調に減衰してますね。しかし、前回同様、分割が頭打ちになっているかどうかは、正解率で見てみましょう…
どん!
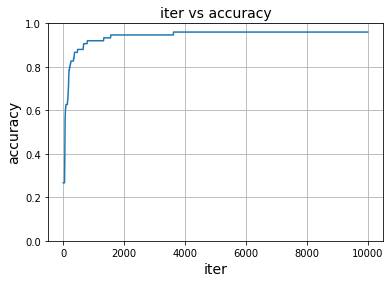
4,000回手前くらいで頭打ちになっていますね。この「正解率で収束を見る」という視点、過学習の見極めの参考になる感じですかねー。
ちなみに、正解率を出すためには当然「正解」がなにかという定義がなされていないといけません。前回の2値問題のときは「予測値が0.5より大きいか小さいか」でしたが、今回は…「予測値ベクトルの中でどの成分の値が一番大きいか」ってことになります。例えば、\( (yp_0,yp_1,yp_2) = (0.1,0.7,0.2) \)って場合、インデックスで言う「1番目」のところが正解値ってことになりますね。
最後に、決定境界についてです。
予測値の出し方が、上に書いたように「一番確率が大きいやつを採用する」方式なので、線を引くというのに若干無理やり感がありますが、がんばって引いてみるとこんな感じになるようです…
どん!
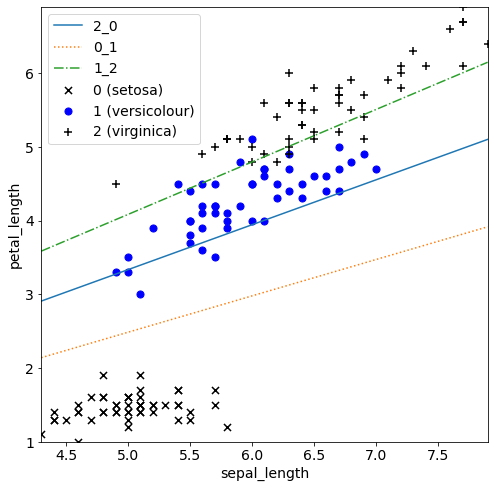
うん、確かにこうして見ると可視性が一気に高まりますね。
ちなみに、あくまでも2つの正解値同士の境界しか引けないので、3本の線が引かれていますね。今回のデータセットは割とキレイに割れているので、「2_0」の線はほとんど意味をなしていない感じはありますかねー。setosaとvirsinicaの違いは明確…ということになるでしょうかね。
ということで
いやー、ついに多値分類の章も終わりました。
ここまでで、本書の80%くらいを進めてきたことになります。気づけばこの記事ももう28回目かー(しみじみ)。
さて、実践編もついに最後の章ですね。次の章は…「ディープラーニングモデル」!ついにここまで来ました。がんばっていくぞー、おー!
ではまた。