どうも、カタミチです。
毎日更新のつもりが、1ヶ月も経たないうちに1日飛んでしまいました(汗)
今日も「ディープラーニング G検定(ジェネラリスト)公式テキスト 第2版」(以降、『当書』)で勉強やっていきますかねー。
サポートベクターマシン
サポートベクターマシンは、高度な数学理論に支えられた手法、とあります。確かに、調べてみると色々と難解な話が出てきたので、とりあえずそっ閉じしました(汗)
ただ、ディープラーニングが考えられる以前は機械学習において最も人気のあった手法のひとつだった…らしいです。
得意なのはどうやら分類問題のようです。
異なるクラスの各データ点との距離が最大となるような境界線を求める事でパターン分類を行う。この距離の事をマージンと言い、これを最大化する。
というのが考え方のようです。
とりあえず、こんなイメージ。
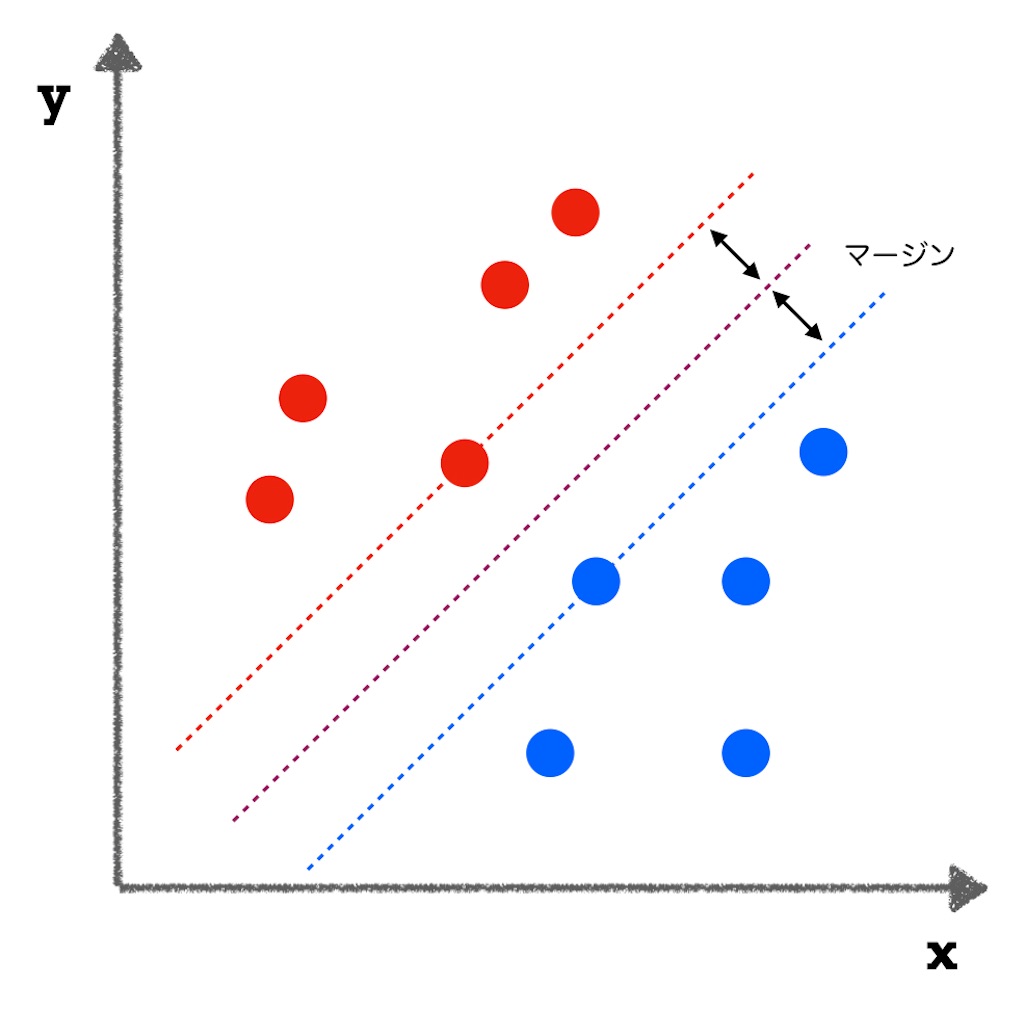
例えば、点がそれぞれアメリカ人を表していると仮定して、赤い点が「共和党派」、青い点が「民主党派」だとしましょう(突然の政治ネタ)。xが何の値でyが何の値かは…妄想で埋めてください。
いずれにせよ、赤の点の中には最も青陣営に近い点があり、青の点の中には最も赤陣営に近い点があります。これらのデータの真ん中を通るような線で分類する…というのが基本的な考え方です。
分類問題では、ロジスティック回帰や決定木を用いた分析も使えましたが、サポートベクターマシンの特徴は、グループを挟んでなるべく真ん中っぽいところに線を引いて分類する、ということみたいですね。
…で、これだけなら単純なんですが、サポートベクターマシンでは「高次元」のデータにも対応してたり、線形分類できない(直線で分けられない)といったデータにも対応してます。
特に後者については、カーネルトリックを使って計算が複雑にならないように式変形する…というテクニックが必要なようです。
例えば、こんな分布。
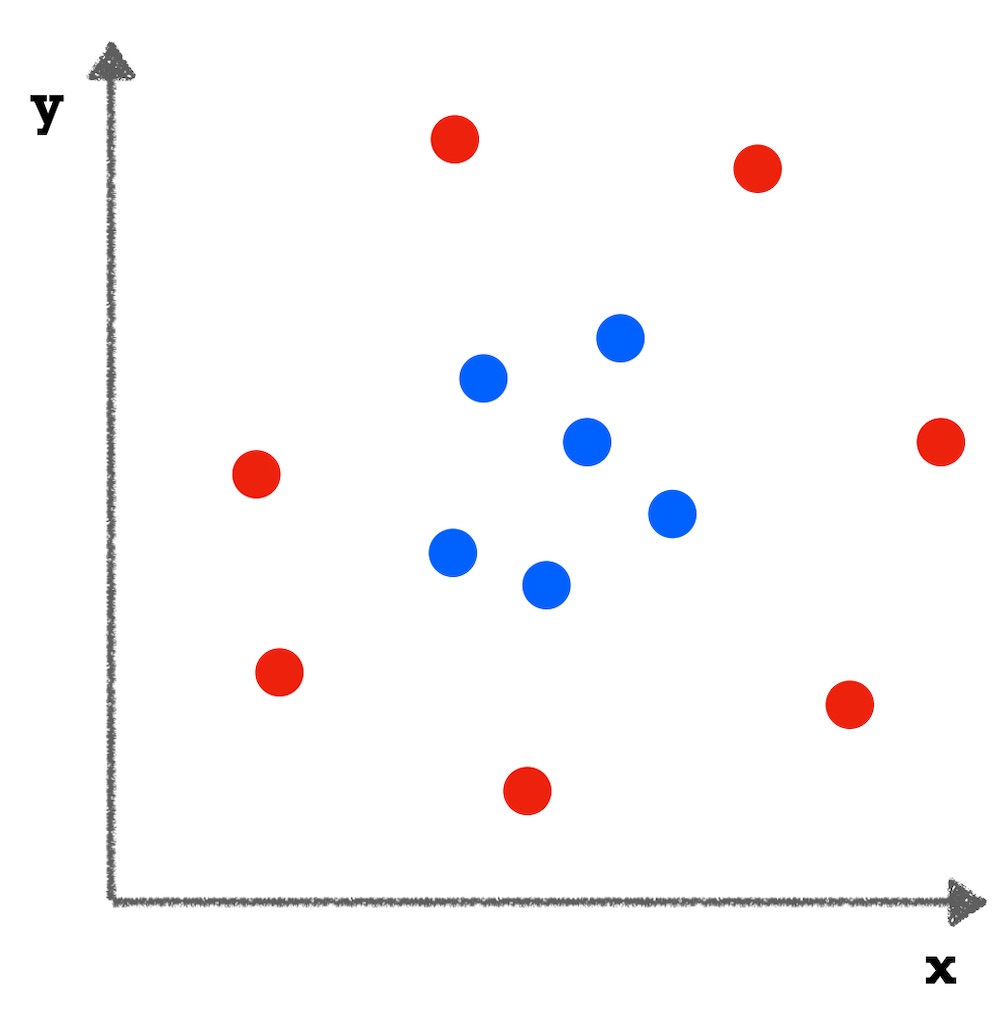
どう考えても直線では分けられそうにありません。そこで、カーネルトリックを使うらしいです。カーネルトリックを使って別の空間に移すことで線形分類ができるようになる…らしいです。呪術廻戦の領域展開みたいな感じですかね(知らんがな)
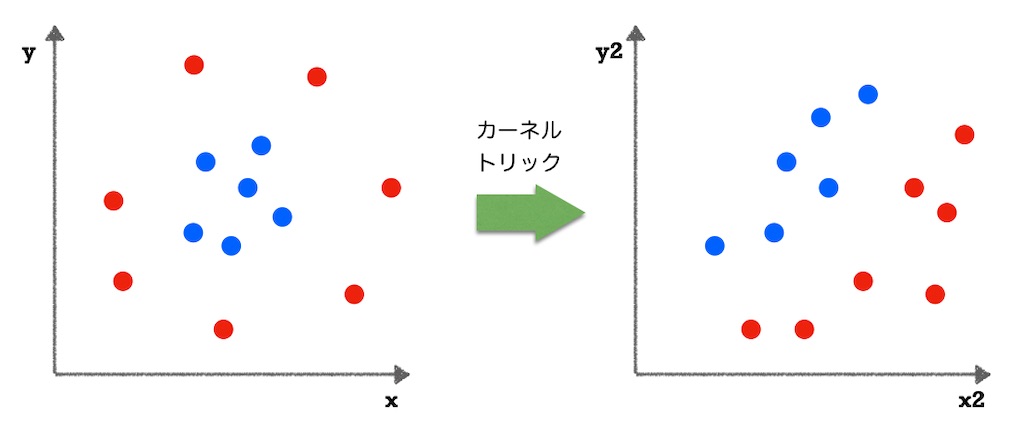
うむ、何となくイメージは分かりますが、どうやればいいかはさっぱりですねー。まぁとりあえずイメージだけ分かっておけばいいですかね。
ということで
教師あり学習の手法も、「線形回帰」「ロジスティック回帰」「ランダムフォレスト」「ブースティング」「サポートベクターマシン」と5個見てきました。残りは2つですね。
引き続き頑張っていきますかねー
ではまた。
勉強に使ってる書籍はこちら↓
深層学習教科書 ディープラーニング G検定(ジェネラリスト)公式テキスト 第2版