どうも、カタミチです。
さて、ようやく5章に入りました。5章は「ディープラーニングの概要」です。いよいよ核心に迫っていく感じですかねー。
まずは、ディープラーニングの基本。
多層パーセプトロン
まず多層パーセプトロンの復習をさらっと。これは、ニューラルネットワークの基本形で、単純パーセプトロンに隠れ層を追加して多層化したものでしたね。単純パーセプトロンでは線形分類しかできなかったところに、隠れ層という新たな「関数」を追加することで、非線形分類ができるようになったものです。
ディープラーニングとは
さてさて、ではディープラーニングとは何かというと…
簡単に言うと、隠れ層を増やしたニューラルネットワークです。多層パーセプトロンの層が多い、つまり層が深いから深層学習とも呼ばれるようです。この点も、以前の章で少し出てきましたね。
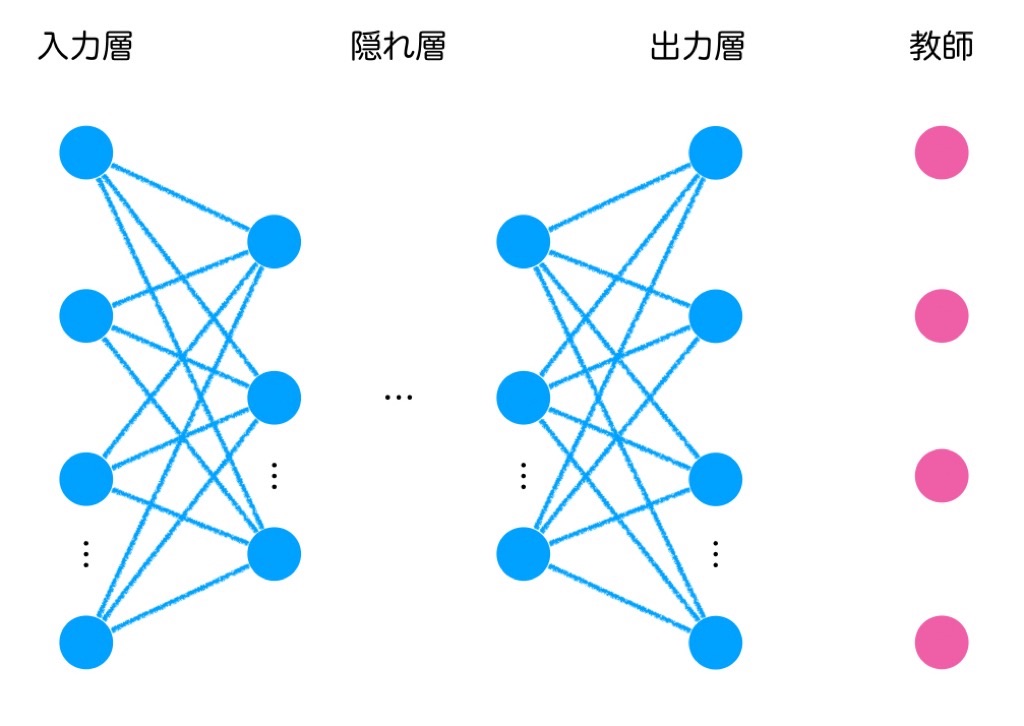
ただこれはあくまでディープラーニングの基本形だそうです。詳しくは6章に書かれているようですが、基本形意外にも様々なモデルが考えられているようですね。
既存のニューラルネットワークにおける問題
隠れ層を増やすというアイデア自体は昔から考えられていたはずなのに、なぜ今頃になって話題になったのか…?
これも、歴史の章にある程度書かれていたので復習な感じですが、ネットワークを深くできなかったんですね。ニューラルネットワークでは、モデルの予測結果と実際の正解値との誤差をネットワークの出力層から入力層に逆向きにフィードバックさせる形でネットワークの重みを更新する誤差逆伝播法を使うのですが、ネットワークを深くすると誤差が最後まで正しく反映されない結果が得られたのです。
問題の根は、ニューラルネットワークの活性化関数として使われているシグモイド関数の特性にありました。誤差逆伝播法では、出力層から遡って隠れ層の重みを更新していくのですが、この際に微分が用いられます。(ちなみに、誤差逆伝播法の数式について少し勉強してみたんですが、数学シロウトにはなかなか厳しかったですね…。改めてちゃんと勉強しようと思いました。)
で、シグモイド関数を微分すると、最大値が0.25にしかなりません。これは1よりもだいぶ小さいため、隠れ層を遡るごとにどんどんこの値は小さくなっていくわけです。これは、勾配消失問題と呼ばれ、ニューラルネットワークを深層にするための大きな妨げになっていました。
ということで
今回は、以前のおさらいのような感じの内容でしたね。果たしてディープラーニングは、勾配消失問題をどう解決したのか…?それが明かされるのが次の節ということですかねー。楽しみです(^-^)
ではまた。
勉強に使ってる書籍はこちら↓
深層学習教科書 ディープラーニング G検定(ジェネラリスト)公式テキスト 第2版