どうも、カタミチです。
前回は、モデルを評価する際のデータの扱いについての話でしたが、今回は評価指標についての話です。
正解率・適合率・再現率・F値
例えば、10,000枚のイヌ、オオカミの画像を学習させた上で、2,000枚の画像がイヌなのかオオカミなのかを予測する分類問題を考えた場合、訓練データが10,000、テストデータが2,000ということになります。
このとき、実際の値と予測値のパターンは以下の4つですね。
1. 予測がイヌで実際もイヌ
2. 予測がイヌで実際はオオカミ
3. 予測がオオカミで実際はイヌ
4. 予測がオオカミで実際もオオカミ
イヌをPositive、オオカミをNegativeとした場合、以下のような表になります。
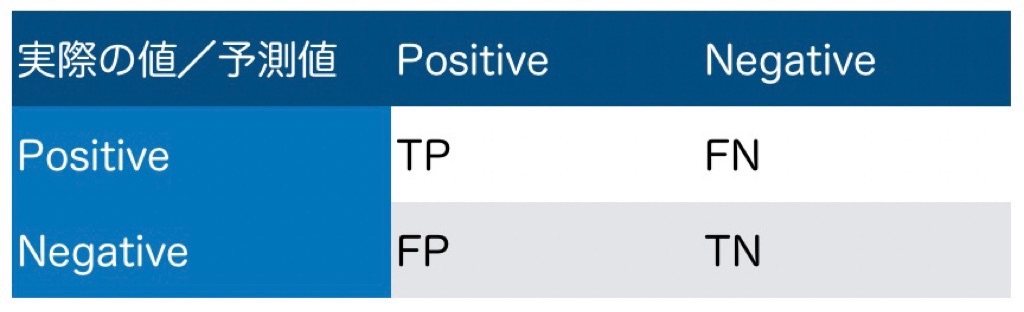
ここで…
TP = True Positive(真陽性)、FN = False Negative(偽陰性)、FP = False Positive(偽陽性)、TN = True Negative(真陰性)
と用語付けされています。
予測が当たっているのは真陽性と真陰性となりますね。つまり、正解率(accuracy)を式で表すと…
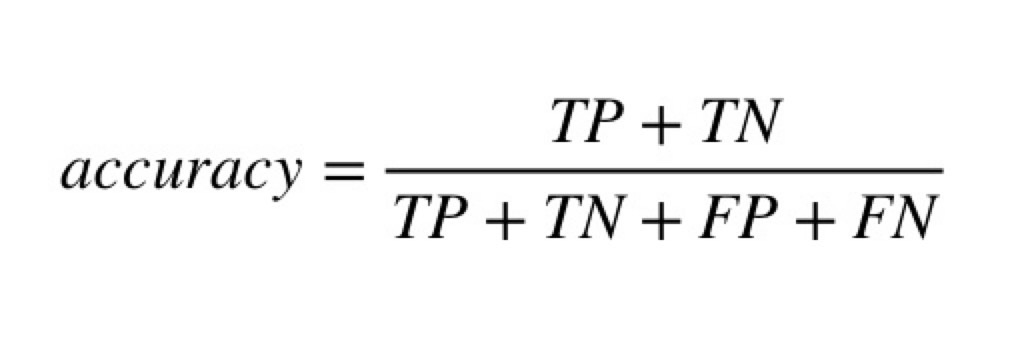
こうなります。これはまぁ分かりやすいですね。続いて、適合率(precision)。予測がPositiveの中で実際にPositiveだったものの割合です。式は…

こう。これも分かりやすいですね。
次に再現率(recall)。実際にPositiveであるものの中で、Positiveだと予測できた割合のことで…
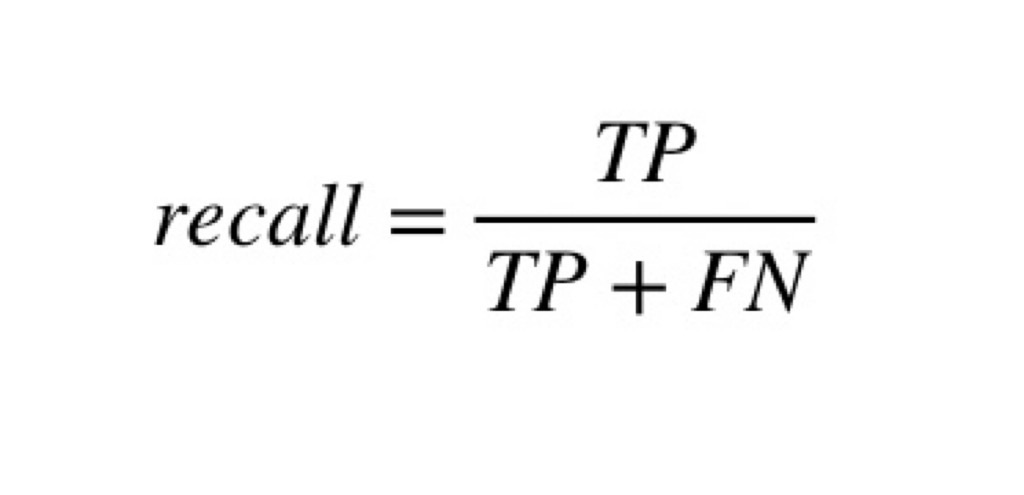
こうです。FNは、False Negative。つまり、Negativeだと誤って認識した、ということで実際の値はPositiveということになります。ゆえに分母はTP+FNで実際のPositive全量を表せるわけですね。
最後にF値(F measure)。
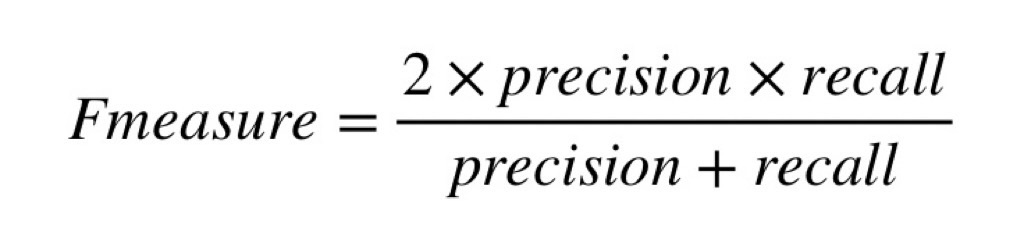
何だか、これまでの仲間が一気に集合した感がありますね(ふむ)
適合率と再現率の調和平均ですね。…調和平均?
調和平均とは「逆数の平均の逆数」を表す数学用語ですね。念の為計算してみると、上の式になります。なぜこの数値が評価にいい感じに使えるのか?はよく分かりませんが、ともかくモデルを評価する指標のひとつとして使われるようです。
さて、ざっと指標を見てきましたが、これらの指標は目的に沿った指標を選択するということが大事なようですね。ちなみに、訓練データに対して指標値(例えば正解率)が高かったとしても、テストデータに対して低いのだとすると、訓練データにのみ最適化されすぎてしまっている状態になっています。これを過学習と言います。なるほど、やりすぎも良くないってことですかね…。
この過学習を防ぐテクニックとして、正則化というものがあります。学習の際に用いる式に項を追加することでとりうる重みの値を制限する…らしいんですが、イメージがつかめません(汗)。とりあえず言葉だけ覚えておくことにしよう…。
ちなみに、正則化しすぎると全体の予測性能が低下してしまうことがあり、これを未学習と言うようです。人生、なかなかままならないものですね(哲学)
正則化を適用した手法に、ラッソ回帰、リッジ回帰、Elastic Netなどがあるようですが、とりあえず用語だけ覚えておきますかねー。
ROC曲線とAUC
さて、上の節では4つの指標が出てきましたが、また別の観点でモデル性能を評価するものとして、ROC曲線、AUCがあります。
ROC曲線は、教師あり学習の手法として出てきた「ロジスティック回帰」においての評価に関するものです。ロジスティック回帰では、モデルの出力が確率で表現されており、閾値(基本的には0.5)を用いて正例か負例かに分類しますが、この閾値を0から1まで変化させていった場合、予測の当たり外れがどのように変化していくのかを表したものが、ROC曲線です。
ROC曲線は、横軸にFPR、縦軸にTPRをとり、閾値を0から1に変化させていった際の両者の値をプロットしていったものを指します。TPR=TP/(TP+FN)、FPR=FP/(FP+TN)であり、TPRは全Posirive中、正しくPositiveと評価された割合で、FPRは全Negative中、Positiveと誤って評価された割合ですね。以下のような図になります。
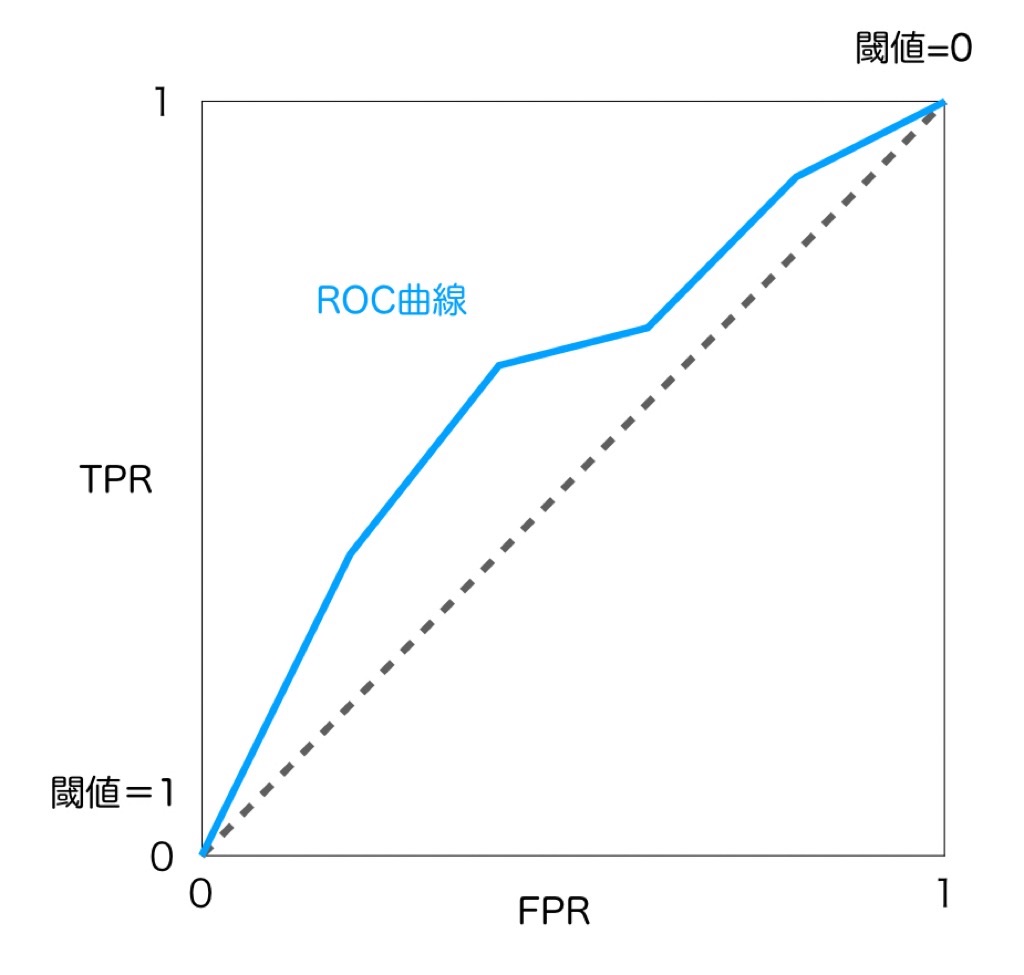
…曲線と言いつつガタガタですが、実際こんな感じらしいです(ふむ)。より左に、より上に張り付いているほどモデル性能が高いということになります。また、このROC曲線の下部の面積をAUCと呼ぶようです。このAUCが1に近いほどモデル性能が高いことを表す…ということで、数値的にも評価できるようになります。
モデルの解釈
実は、多くの機械学習のモデルは、予測の判断根拠を説明するのを苦手としています。複雑な入出力の関係を予測することを可能にするのだから、モデル自体も複雑で解釈が難しい…というのは、ここまで勉強してくると想像がつきます。
しかしやはり、解釈できないと気持ち悪い…という気持ちになる人がいるのも分かります。「独自に編み出した機械学習のモデルを使って、今買うと確実に大儲けできる金融商品をあなただけにそっと教えます!」と言われても、ちょっと信じられないですよね。…というかそれ、詐欺です、間違いなく。
なので、モデルを説明しようとする努力はなされるべきだ、ということはあるようです。例えば、前に出てきたランダムフォレストや勾配ブースティングといった決定木ベースのモデルは、特徴量の重要度を算出することができます。また、LIMEという手法で、もともとは複雑なモデルを単純な線形モデルに近似することによって説明性をもたせようとしています。用語だけの紹介でしたが、他にもSHAPといった手法もあるみたいですね。
モデルの選択と情報量
どんなモデルを試せるのか?については多くの選択肢があり、また、モデルの複雑さも様々調整できます。ここで一つの参考になるのが、オッカムの剃刀という指針です。なかなかご機嫌なネーミングですがこれ、オッカムという哲学者が、「必要なしに多くのものを定立してはならない」と言って、根拠のない要素をバッサバッサと切り落としていったことからこの名がついたようです。…日常でも使ってみたい言葉ですね。
機械学習の世界でも、モデルを複雑にすればするほど過学習の可能性もあるため、オッカムの剃刀の考え方を頭に入れつつ選択肢を選んでいくべきなのでしょうね。
では、解きたいタスクに対して実際にモデルをどれくらい複雑にすればよいか?という問題に対してのひとつの目安となるのが、赤池情報量基準(AIC)です。…アカイケ!どうやら日本人の赤池さんが考案したようです。モデルの複雑さと予測精度のバランスを考えたものだ…とのことです。
ということで
これでようやく4章まで勉強を終える事ができました(ふう)
ということで、残るは5章、6章、7章、Appendix…なのですが、試算してみるとどうやら今のペースではとうてい試験までに間に合わない!!
…さて、どうしたもんですかねー。本当は今のままノンビリやりたいんですが、13,200円を棒に振るのもなぁ。とりあえず、がんばれるだけ頑張ってみたいと思います。
ではまた。
勉強に使ってる書籍はこちら↓
深層学習教科書 ディープラーニング G検定(ジェネラリスト)公式テキスト 第2版