どうも、カタミチです。
さて、今回から「教師なし学習」の代表的な手法に入ります。紹介されているのは5つですね。
・階層なしクラスタリング(k-means法)
・階層ありクラスタリング(ウォード法)
・主成分分析
・協調フィルタリング
・トピックモデル
まず「教師なし学習」は、入力データにある構造や特徴をつかむものでしたね。さて、行ってみましょう。
階層なしクラスタリング(k-means法)
k-means法は、データをk個のグループに分けることを目的としているようです。各グループはクラスタと呼ばれます。特に最近はよく聞きますね、クラスタって言葉自体は。
アプローチはシンプルで…
- まずは適当に各データをk個のクラスタに振り分ける
- 各クラスタの重心を求める
- 求まったk個の重心と各データとの距離を求め、各データを最も距離が近い重心に対応するクラスタに振り分け直す
- 重心の位置が(ほぼ)変化しなくなるまで2,3を繰り返す
だそうです。うん、確かにシンプルでイメージしやすいですね。唯一「重心」の求め方だけ分かりませんが、まぁ少し勉強すればできそうな気はします。
とりあえずこんな絵でイメージを持っておけばいいみたいです(適当)
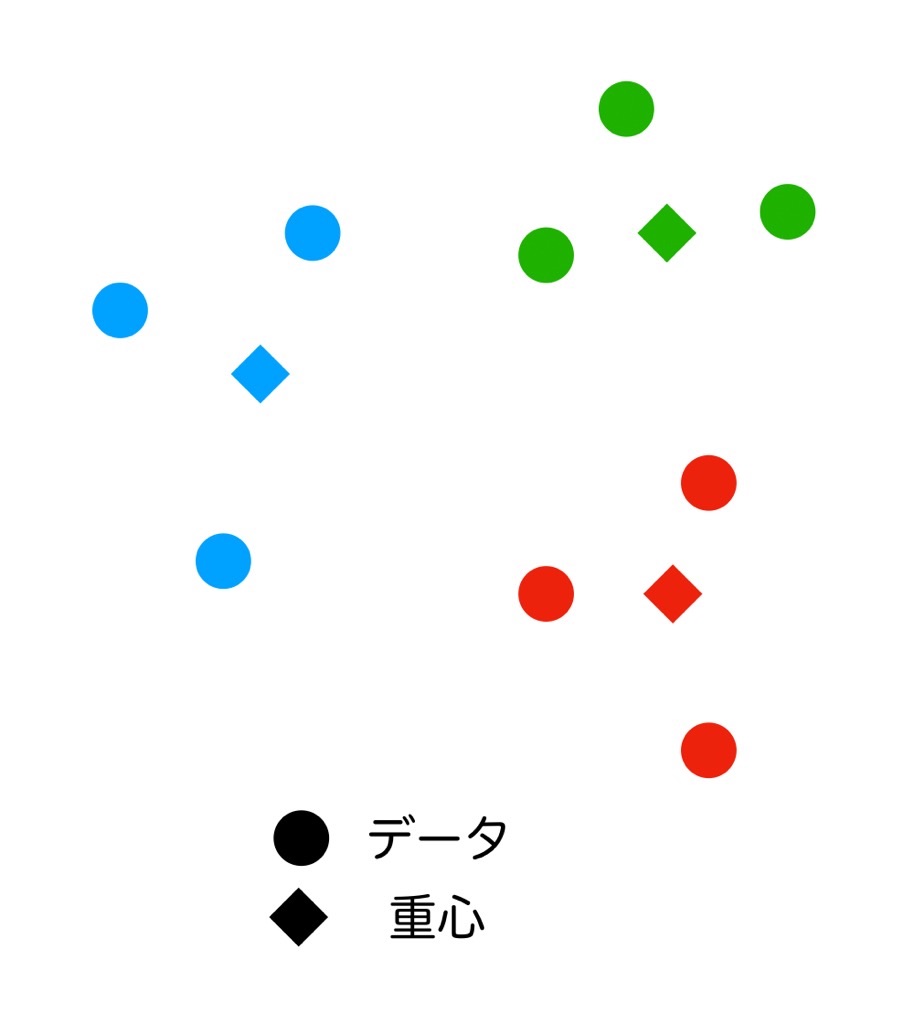
階層ありクラスタリング(ウォード法)
さて、次は「階層あり」って事ですが、階層なしと何が違うのかなー、と思って見てみると、そこから更にクラスタの階層構造を求めるまで行うのがこのウォード法だそうです。つまり、違うってより更に先に進むって感じですかね。
手順はこちらも簡単。最も距離が近い2つのデータを選びそれらを1つのクラスタにまとめる、という処理を繰り返す、以上。
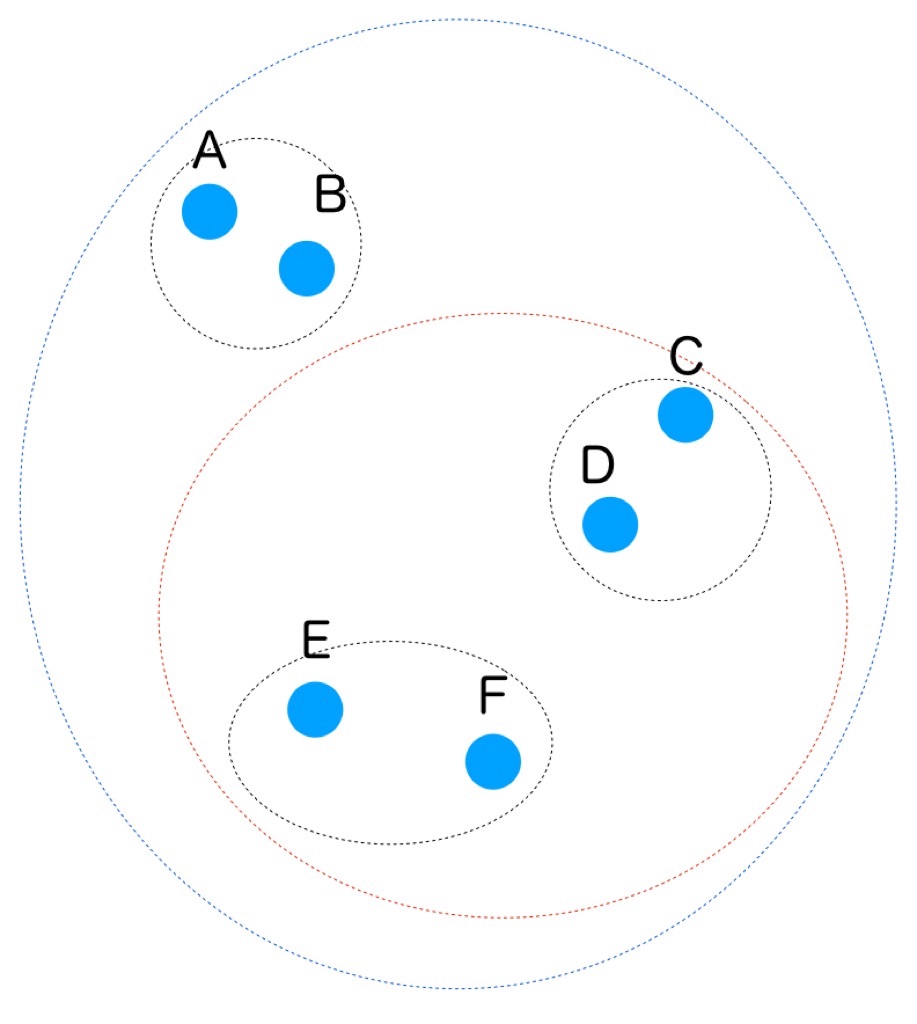
↑こんなイメージですね。しかし、k-means法でクラスタに分けた後で隣同士をくっつけたら、別のクラスタにいる2つのデータがペアになってしまう事もあるのでは…?と思ったんですが、そのあたりについては特に言及はありませんでした(汗)。余談ですが、私が住んでるところから一番近い保育園が、隣の行政区にあるお陰で、そこに娘を入れようと思っても待機児童としての優先度が低い…という事がありました。…余談終わり。
ともあれ「じゃんけん列車」的にくっつけていく事だけは分かりました、はい。
主成分分析
続いては主成分分析です。
…うっっ、統計検定の勉強をしてた頃に出てきた記憶が…。5年前の記憶を呼び覚ますのだ!(呼び覚ませませんでした)
データの特徴量の関係=相関を分析する事で構造をつかむ手法、とのことです。
機会学習で用いる特徴量は次元が多くなりがちなので、次元削減するために用いる事が多いようです。強い相関を持つ特徴量同士を見つけて、どちらかを削っていく感じですね。
主成分分析以外にも、特異値分解(SVD)、多次元尺度構成法(MDS)、可視化によく使うt-SNEなどがあるようです。
うーん、名前だけの紹介なのでイメージが湧かないですねー。余裕ができたらそれぞれもう少し深く理解したいところです。
協調フィルタリング
4つ目は協調フィルタリング。レコメンデーションに用いられる手法のようです。…ん?レコメンデーションって「それ買った人は、これも買ってるよ!」ってやつですよね。値の推定してるから教師あり学習なのでは…?(混乱)
ユーザー間の類似度(同じ商品のレビュー評価の相関係数など)を定義して類似度の高いユーザーかわ購入済みの商品をレコメンドしてくる…というようなやり方と、ユーザーではなく商品側に特徴量を付与して似ている商品をレコメンドする、コンテンツベースフィルタリングというやり方があります。
前者は、ある程度データが無いとレコメンドできず、コールドスタート問題と呼ばれているようです。まぁ、だからといって後者のコンテンツベースフィルタリングが優れているかというと必ずしもそうではない…というのは、イメージとしても分かる話です。
トピックモデル
最後はトピックモデルです。
クラスタリングを行うという点ではk-means法やウォード法と同じなんですが、トピックモデルは複数のクラスタにデータを分類するのが特徴です。「タグ」みたいなイメージですかね。
代表的な手法に潜在的ディリクレ配分法(LDA)があり、トピックモデルといえばLDAという感じらしいです。
ということで
教師あり学習はかなり記事を刻みましたが、教師なし学習は一気に行きました。
演習問題があったわけではなく、手法の名前だけの紹介なのでイマイチ掴みきれた気がしませんが、ひとまずはこんなところですかねー。
ちなみに、この記事書いてる途中に70%くらいの内容が消えるという事件があって、途中から書き直しました(泣)。まぁ、何度も書く事で記憶に定着しやすくなるからいいんだ…。
ではまた。
勉強に使ってる書籍はこちら↓
深層学習教科書 ディープラーニング G検定(ジェネラリスト)公式テキスト 第2版